1.ブリッジ回路
【例題】
下の図の回路で導線ABに流れる電流の向きと大きさを求めよ。

①回路を書き換える
まずは分かりやすくするために、下の図のように回路を書き換えてみます。

このときR₁~R₄に流れる電流の大きさを考えます。
②回路全体の抵抗を求める
まず左側(R₁とR₂)の部分と右側(R₃とR₄)の部分の合成抵抗をそれぞれ求めましょう。
並列につながっている部分の合成抵抗は

で求められます。
よって左側(R₁とR₂)の部分は
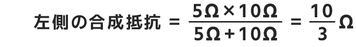
右側(R₃とR₄)の部分は

となります。↓

よって回路全体の抵抗は

となります。
③回路全体に流れる電流を求める
次に回路全体に流れる電流を求めましょう。
電源の電圧が28V、回路全体の抵抗が14/3Ωなので、
オームの法則より

となります。↓

④抵抗1つ1つに流れる電流を求める
ではR₁~R₄に流れる電流はそれぞれ何Aか求めましょう。
このとき
並列回路では「抵抗の逆比=電流の比」となる
ことを利用するとすばやく求めることができます。
左側(R₁とR₂)を見てみます。
R₁の抵抗:R₂の抵抗=5Ω:10Ω=1:2
なので
R₁の電流:R₂の電流=2:1
となります。↓

6Aが2:1に分かれて流れていくことになるので

となります。↓

右側(R₃とR₄)も同じように電流を求めましょう。
R₃の抵抗:R₄の抵抗=2Ω:4Ω=1:2
なので
R₃の電流:R₄の電流=2:1
です。
6Aが2:1に分かれて流れていくことになるので

となります。
以上より各抵抗に流れる電流は↓のようになっていることがわかりました。

⑤もとの回路に電流を書き戻す
先ほど求めた電流をもとの回路に書き加えます。↓

ここでABの部分を考えてみます。
R₁が4A、R₃も4Aです。
R₁に流れた電流4Aが、そのままR₃に流れたのです。
同じようにR₂が2A、R₄も2Aです。
R₂に流れた電流2Aが、そのままR₄に流れています。
つまりABの部分にはまったく電流が流れていないのです。
よってABの部分の電流は0Aとなります。
ここで回路の抵抗に注目すると↓のようになっていることがわかります。

R₁×R₄=R₂×R₃
このようなとき、ABの部分には電流が流れないのです。
もし問題を解く前に上の式が成り立っていることに気づけば、AB部分の電流は0Aとすぐ判断できます。
また次のようにAB部分の導線を省略して考えることも可能です。

R₁×R₄=R₂×R₃となっているとき、AB部分に電流は流れない。

