1.ブリッジ回路
↓のような回路をブリッジ回路といいます。

通常のオームの法則を使って解く電流回路の問題だと思うと解けないのが厄介なところです。
高校入試で出題されるのは主に2パターンです。
▼パターン1

▼パターン2

重要なのは中央の部分に流れる電流の向きと大きさです。
抵抗によっては上向きの電流、または下向きの電流もあり得ます。
また電流が流れないということもあり得ます。
今回はパターン1の方を見ていきましょう。
2.ブリッジ回路の解法
【例題】
下の図の回路で導線ABに流れる電流の向きと大きさを求めよ。

①回路を書き換える
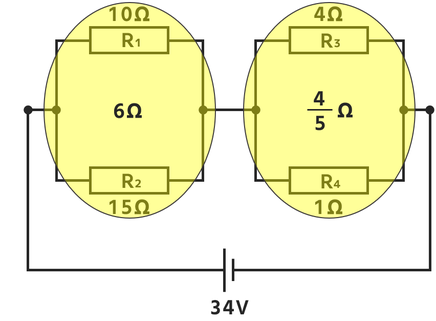
まずは分かりやすくするために、下の図のように回路を書き換えてみます。

このときR₁~R₄に流れる電流の大きさを考えます。
②回路全体の抵抗を求める
まず左側(R₁とR₂)の部分と右側(R₃とR₄)の部分の合成抵抗をそれぞれ求めましょう。
並列につながっている部分の合成抵抗の求め方は

です。
よって左側(R₁とR₂)の部分は

右側(R₃とR₄)の部分は
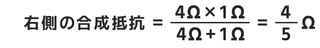
となります。↓
よって回路全体の抵抗は

となります。
③回路全体に流れる電流を求める
次に回路全体に流れる電流を求めましょう。
電源の電圧が34V、回路全体の抵抗が34/5Ωなので、
オームの法則より

となります。↓

④抵抗1つ1つに流れる電流を求める
ではR₁~R₄に流れる電流はそれぞれ何Aか求めましょう。
このとき
並列回路では「抵抗の逆比=電流の比」となる
ことを利用するとすばやく求めることができます。
左側(R₁とR₂)を見てみます。
R₁の抵抗:R₂の抵抗=10Ω:15Ω=2:3
なので
R₁の電流:R₂の電流=3:2
となります。↓

5Aが3:2に分かれて流れていくことになるので

となります。↓

右側(R₃とR₄)も同じように電流を求めましょう。
R₃の抵抗:R₄の抵抗=4Ω:1Ω=4:1
なので
R₃の電流:R₄の電流=1:4
です。
5Aが1:4に分かれて流れていくことになるので

となります。
以上より各抵抗に流れる電流は↓のようになっていることがわかりました。

⑤もとの回路に電流を書き戻す
先ほど求めた電流をもとの回路に書き加えます。↓

ここでABの部分を考えてみます。
R₁には3Aの電流が流れているのに対し、R₃には1Aの電流しか流れていません。
このことから、2Aの電流がAからBへと進んでいったと考えられます。
R₂に流れた電流は2A。
ここに先ほどの電流2Aが合流して、R₄に4A流れているわけです。↓

よってABの部分には
AからBへ2Aの電流が流れていることになります。
ブリッジ回路の問題は
①回路を書き換える
②回路全体の抵抗を求める
③回路全体に流れる電流を求める
④抵抗1つ1つに流れる電流を求める
⑤もとの回路に電流を書き戻す
の手順で解きましょう。

