1.鏡に映る像
例題
↓の図は、鏡とその前に置かれたA~Eの5つの物体、および観測者の目の位置を上から見たものである。
観測者が鏡を見たとき、鏡に映る像を見ることができないのはA~Eのどれか。

反射の問題で大事なのは、
①鏡に引いた垂線
②像の位置を正しく作図する
ということです。
この場合は
②像の位置を正しく作図する
ことが重要です。
像は鏡を対称の軸として線対称な位置にできます。
作図すると↓のようになります。
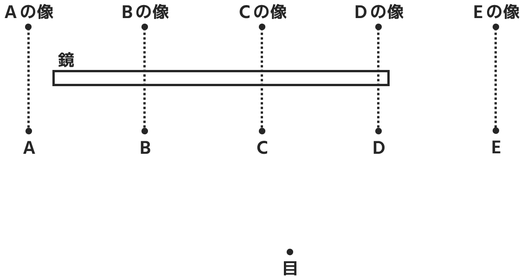
この像を見ることができるかどうかは、鏡の両端に向かって線を引いてみるとわかります。
↓の図の赤色の部分に像があるかどうかを確認しましょう。
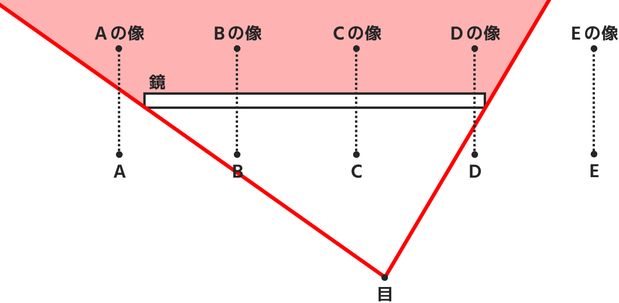
赤色の部分にあれば、その像は「鏡に映った像」として見ることができます。
よってこの場合は、A・B・C・Dの像は見ることができます。
一方でEの像は見ることができません。
したがって正解はEとなります。
2.合わせ鏡
次のように鏡Aと鏡Bを90度の角をなすように置きました。
その間に物体Pと観測者がいます。

このとき、観測者はPの像をどのようにして見ることができるのでしょうか。
鏡Aで反射する光
Pが鏡Aに映るときを考えます。
Pの像P’₁を鏡Aに対して線対称な位置に作図します。↓

P’₁を利用して光の通り道を作図すると↓のようになります。

鏡Bで反射する光
Pが鏡Bに映るときを考えます。
Pの像P’₂を鏡Bに対して線対称な位置に作図します。↓

P’₂を利用して光の通り道を作図すると↓のようになります。

鏡A・Bの両方に反射する光
ここまでで↓の図のように、2つの像P’₁とP’₂があることがわかりました。
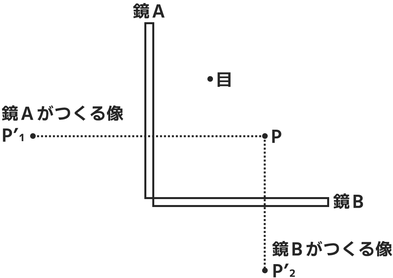
鏡AにはP’₁という像が映っています。
しかし映るのはP’₁だけではありません。
鏡Aには鏡Bも映りこんでいるはずです。
その像は↓のようになります。

鏡Aには、Pの像P’₁と鏡Bの像が同時に映りこんでいるのです。
そしてP’₁は「鏡Bの像」にも映りこむはずです。↓

同じことを鏡Bの方でも考えてみましょう。
鏡Bには、Pの像P’₂と鏡Aの像が同時に映りこんでいることになります。↓

そしてP’₂は「鏡Aの像」に映りこみます。↓

これは先ほどの像と重なります。
つまりまとめると↓のようになっています。

このように90度に並べた2枚の鏡には、像が3つできるのです。
この3つ目の像P’₃から出た光が目に入るようすを作図してみましょう。
まずP’₃と目を線で結びます。
そうすることで光が反射する点がわかります。↓

この点とP’₂を結びます。
そうするともう1つ、光が反射する点がわかります。↓

あとはPから直線を引いていきましょう。↓

今回は90度の角をなすように鏡が置かれていました。
この場合、できる像は3つです。
しかしほかの角度であれば、できる像の数は異なります。
ですが考え方は同じです。
物体だけでなく、鏡の像も考えることがポイントです。

