1.写像公式
●写像公式
以下の図において次の公式が成り立つ。
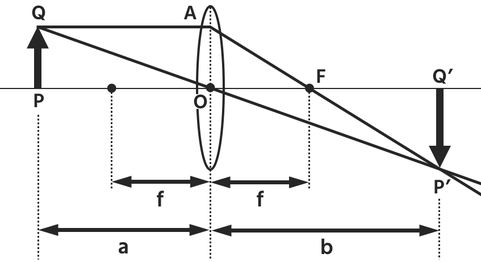

ただしb<0のときは虚像ができていることを表す。
また像の大きさを以下のように求めることができる。

2.写像公式の証明
前項の公式を証明してみましょう。
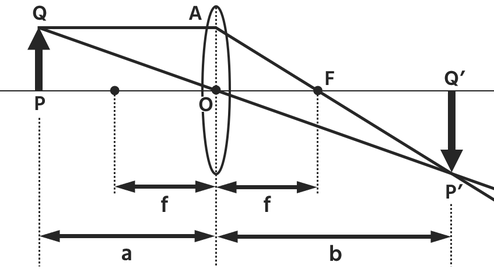
↑の図には三角形がいくつかあります。
うち↓の図のような三角形を考えます。

赤い三角形どうしは相似です(2組の角がそれぞれ等しい)。
つまり△OQP∽△OP'Q'
この相似比は
PO:Q'O=a:b
よって対応する辺であるQPとP'Q'の比も
QP:P'Q'=a:b
となります。
次に↓の図の三角形を考えます。

青い三角形どうしは相似です(2組の角がそれぞれ等しい)。
つまり△AOF∽△P'Q'F
この相似比は
OF:Q'F=f:b-f
よって対応する辺であるAOとP'Q'の比も
AO:P'Q'=f:b-f
となります。
ここでAO=QPであることに着目。
QP:P'Q'=a:b
QP:P'Q'=AO:P'Q'=f:b-f
より
a:b=f:b-f
という式が導き出されます。
内項の積と外項の積は等しいので
b×f=a(b-f)
bf=ab-af
両辺をabfで割ると

よって最初に紹介した式、

となります。
この公式を覚えておくと便利ですが、何より重要なのは相似な三角形が隠されていることに気づくことです。
・凸レンズの応用問題は「三角形の相似」を意識しよう。

