1.連結された物体の力学的エネルギー
1kgの物体Aと2kgの物体Bが質量の無視できる糸によってつながれています。
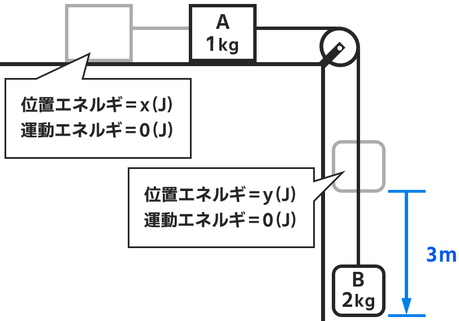
これを↓の図のように、滑車のついた摩擦のない台に置いたとします。

ここで物体Bが3m落下したとき(↓)の物体A、Bの運動エネルギーを考えます。

また以下では100gの物体にはたらく重力は1Nであるとし、空気抵抗も考えないものとします。
この例のような連結された物体の力学的エネルギーは
物体Aの力学的エネルギー+物体Bの力学的エネルギーが保存されます。
言いかえると
連動して動く物体Aと物体Bを1つの物体としてみなし、この物体の力学的エネルギーが保存される
という考え方です。
物体Aだけの力学的エネルギーは保存されなしい、物体Bだけの力学的エネルギーも保存されません。
ではまず、
スタート時の物体Aの位置エネルギーを x(J)
スタート時の物体Bの位置エネルギーを y(J)
物体Bが3m落下した時点での物体Aの運動エネルギーを X(J)
物体Bが3m落下した時点での物体Bの運動エネルギーを Y(J)
とします。
物体Bは3m落下しているので、位置エネルギーが減少します。
その値は
20N×3m=60J
ここで、スタート時の物体A、Bの位置エネルギー・運動エネルギーを表すと
スタート時の物体Aの位置エネルギー=x(J)
スタート時の物体Aの運動エネルギー=0(J)
スタート時の物体Bの位置エネルギー=y(J)
スタート時の物体Bの運動エネルギー=0(J)
これをあわせると
連結物体の力学的エネルギー=x+y(J)・・・①
となります。
次に、物体Bが3m落下したときの物体A、Bの位置エネルギー・運動エネルギーを表すと
落下したときの物体Aの位置エネルギー=x(J)
落下したときの物体Aの運動エネルギー=X(J)
落下したときの物体Bの位置エネルギー=y-60(J)
落下したときの物体Bの運動エネルギー=Y(J)

これをあわせると
連結物体の力学的エネルギー=x+y+X+Y-60(J)・・・②
となります。
力学的エネルギーの保存により、①と②は等しいので
x+y=x+y+X+Y-60
よって
X+Y=60・・・③
となります。
運動エネルギーは

で求められたので

物体A・Bともに速さは等しいので
X:Y=1:2・・・④
となります。
したがって③、④より
X=20J Y=40J
となります。
このように連結物体どうしの運動エネルギーは質量比によって決まります(速さが同じであるため)。
これをふまえると、文字式を使わずに解くこともできます。
この例のAとBの連結物体は60Jの位置エネルギーを失いました。↓

それ以外に失われたエネルギーはありません。
ということはこの60Jは運動エネルギーへと移り変わるはずです。
つまり
物体Aの運動エネルギー+物体Bの運動エネルギー=60J
ということになり
物体Aの運動エネルギー:物体Bの運動エネルギー=1:2
であるので
物体Aの運動エネルギー=20J
物体Bの運動エネルギー=40J
と求めることができます。
連結物体の運動は・・・
・連動して動く物体どうしを1つの物体としてみなし、この物体の力学的エネルギーが保存されると考える。
・連結物体どうしの運動エネルギーは質量比によって決まる。

