1.力学的エネルギー保存の法則
●力学的エネルギー
力学的エネルギー = 位置エネルギー + 運動エネルギー
※つまり位置エネルギーと運動エネルギーの和を力学的エネルギーと言います。
●力学的エネルギー保存の法則
外部から力を受けない限り力学的エネルギーは一定であるということ。
※外部からの力・・・摩擦力や空気抵抗など。
力学的エネルギーは運動の最中、常に一定になります。
※ただし運動のようすを変えるような力(摩擦力や空気抵抗)がはたらいていなければという条件付き。
このきまりを力学的エネルギーの保存、または力学的エネルギー保存の法則といいます。
2.力学的エネルギー保存の法則の使い方
↓の図のようなコースを質量3kgの物体が進んでいくとしましょう。
ここでは摩擦や空気抵抗は考えないものとします。
3kgの小球を10mの高さから、静かに手を離し滑らせます。

ここからA点・B点・C点を通過したときのエネルギーを考えます。
① A点
高さは10mです。
ここで位置エネルギーの公式を使うと
A点での位置エネルギー = 30N×10m = 300J
とわかります。↓
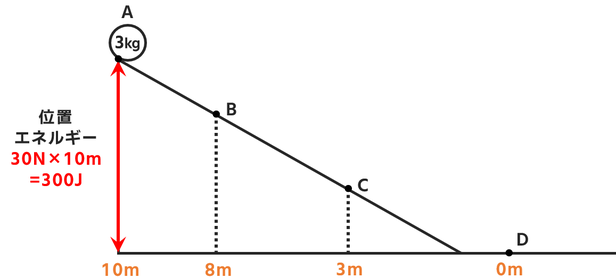
ここでは手を離した瞬間なので、速さはゼロです。
つまり
運動エネルギー=0J
です。
よって
力学的エネルギー = 位置エネルギー + 運動エネルギー = 300J
とわかります。↓

この後も力学的エネルギーの保存という決まりによって
力学的エネルギーは300Jのまま保存されます(変化しない)。
② B点を通過した瞬間
B点は8mの高さなので
位置エネルギーの公式を使うと
B点での位置エネルギー = 30N×8m = 240J
となります。↓

このとき力学的エネルギーは300Jのまま保存されています。
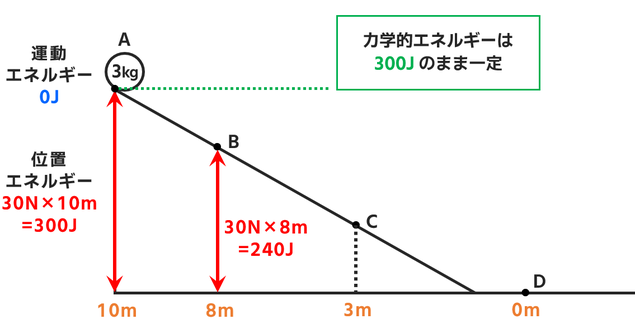
よって
運動エネルギー = 300J - 240J = 60J
となります。↓

③ C点を通過した瞬間
C点は高さ3mなので
C点での位置エネルギー = 30N×3m = 90J
です。↓

ここでも力学的エネルギーは300Jです。(力学的エネルギー保存の法則)

よって
運動エネルギー = 300J - 90J = 210J
となります。↓

運動エネルギーはB点通過時は60J、比べてC点通過時は210Jと大きくなっています。
つまりB点通過時よりC点通過時の方が速さが大きいことがわかりますね。
④ D点を通過した瞬間
D点は高さ0mなので
D点での位置エネルギー = 0J
です。↓

ここでも力学的エネルギーは300Jです。(力学的エネルギー保存の法則)
よって
運動エネルギー = 300J - 0J = 300J
となります。↓

つまりD点でもっとも運動エネルギーが大きい=速さが大きいことになりますね。
このように力学的エネルギーが保存される場合は
運動エネルギー = 力学的エネルギー - 位置エネルギー
として求めることができます。
また高さが低いところほど運動エネルギーが大きく、速さも大きいことになります。
グラフで見てみましょう。
位置エネルギーは次のように変化していました。

一方で運動エネルギーは↓のようなグラフになります。

また力学的エネルギーは保存されているので↓のような一定のグラフになります。
この3つのグラフを1つにまとめてみましょう。↓

このように力学的エネルギーが保存されるならば
・低いところほど運動エネルギーは大きい(=速い)
・位置エネルギーが増えると運動エネルギーは減る
・位置エネルギーが減ると運動エネルギーは増える
・つまり位置エネルギーと運動エネルギーは逆の変化をする
ということになります。
・運動エネルギーは「力学的エネルギーと位置エネルギーの差」で求める。
・図中にエネルギーを図示してみると解きやすい。

