1.時間と速さのグラフ
速さが一定の運動をしている場合
台車が摩擦のない滑らかな面を動いているときを考えます。
そのとき時間と速さの関係は↓の図のようになります。
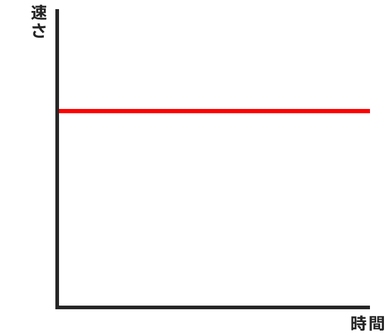
ここで↓のようなグラフで表される運動を考えます。

このグラフは
物体が常に10m/sで動いている
ということを意味しています。
速さ10m/sで等速直線運動をしているということです。
この運動を3秒間行った時の移動距離は

となります。
この式は↓の図の長方形の面積を求める式(=縦×横)と一致します。

このように、速さが一定の運動の「時間と速さのグラフ」では
面積=移動距離
となります。
速さが一定の割合で変化している場合①
時間と速さの関係が↓のようになっている運動を考えます。
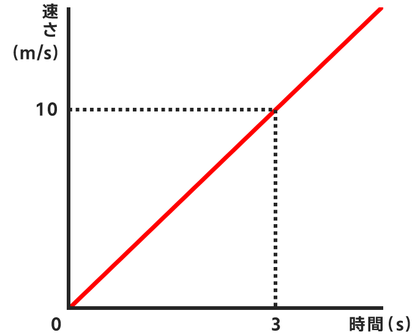
このグラフの意味は
・はじめの速さは0m/s
・時間に比例して速さが大きくなっていく
です。
0秒後の速さは0m/s、3秒後の速さは10m/sですので、この速さの平均をとると5m/sとなります。
よって3秒後までに移動した距離は

となります。
これは↓の図の長方形の面積を意味します。

一方で↓の図の三角形の面積にも等しいことになります。

速さが一定の割合で変化している場合②
時間と速さの関係が↓のようになっている運動を考えます。

このグラフの意味は
・はじめの速さは4m/s
・一定の割合で速さが大きくなっていく
です。
0秒後の速さは4m/s、3秒後の速さは8m/sですので、この速さの平均をとると6m/sとなります。
よって3秒後までに移動した距離は

となります。
これは↓の図の長方形の面積を意味します。

一方で↓の図の台形の面積にも等しいことになります。

以上より、時間と速さの関係を表すグラフでは
グラフと横軸(x軸)の間にできる図形の面積=移動距離となる
と言えます。
例題
下のグラフで表される運動について、次の問いに答えなさい。

(1)0~8秒後までの移動距離はいくらか。
(2)0~8秒後までの平均の速さはいくらか。
【解】
(1)0~8秒後までの移動距離を求めなさい。
この場合の移動距離は↓の図形の面積に等しいので

移動距離は64mとなります。
(2)0~8秒後までの平均の速さを求めなさい。
平均の速さ=距離÷時間なので、0~8秒後までの平均の速さは

よって正解は8m/sとなります。
・時間と速さの関係を表すグラフでは・・・
グラフと横軸(x軸)の間にできる図形の面積=移動距離
となる。

