1.分力を使った力のつり合い
例題
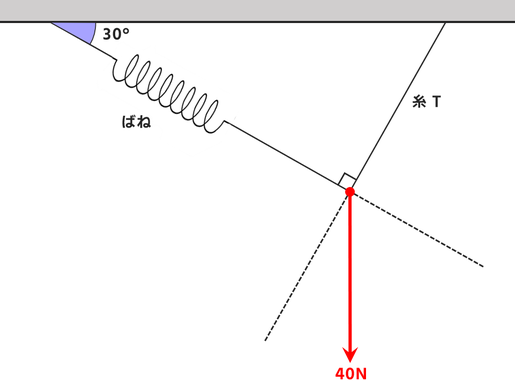
ばね、糸、4kgのおもりを次のようにつなぐと、図の状態で静止した。
このとき、ばね・糸Tに加わる力はそれぞれ何Nか。
ただし100gの物体にはたらく重力を1Nとする。

解法1.糸・ばねの方向に力を分解する
おもりの質量は4kgです。
よってこのおもりには40Nの重力がはたらいています。
この力を↓の図のように糸Tの延長方向・ばねの延長方向に分解することを考えます。
手順に沿って作図すると↓のようになります。

このときできた三角形に注目すると・・・
30度・60度・90度の三角形が隠れています。↓
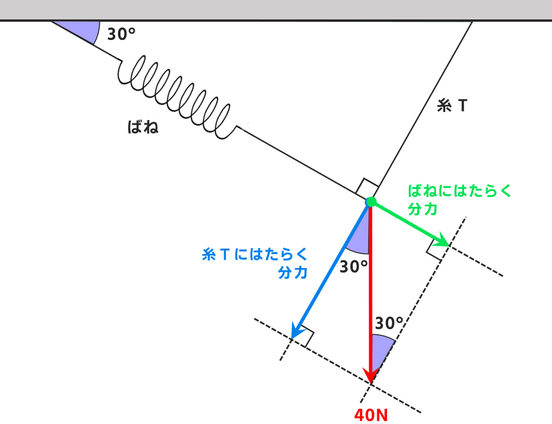
この三角形の辺の比は
1:2:√3
です。↓

よって

となります。↓

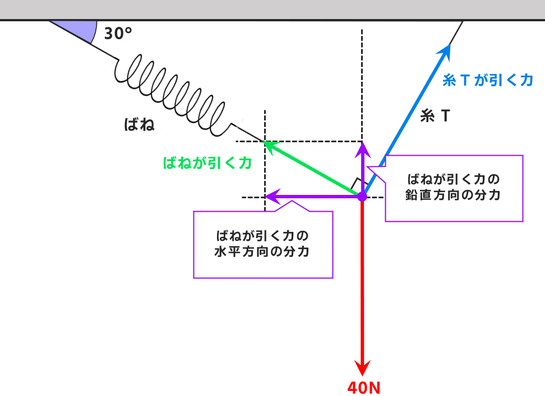
解法2.張力や弾性力を水平・鉛直方向に分解する
張力とは糸が物体を引く力です。
また弾性力とはばねが物体を引く力です。
それぞれを図示すると↓のようになります。

これを水平・鉛直方向に分解します。↓
(水平・・・横方向 鉛直・・・縦方向)

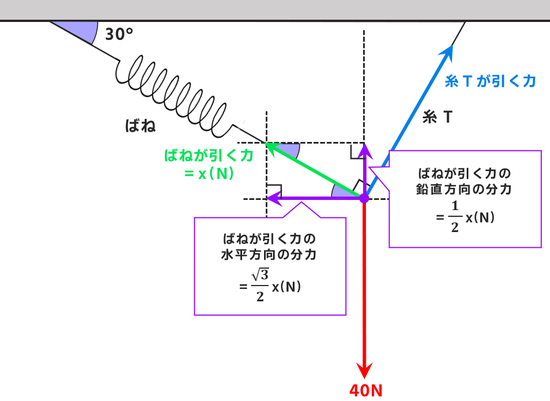
まずはばねが引く力を分解しましょう。↓
ここにも30度・60度・90度の三角形が隠れています。
ばねが引く力をx(N)とすると

と表せます。↓
続いて糸Tが引く力を分解しましょう。
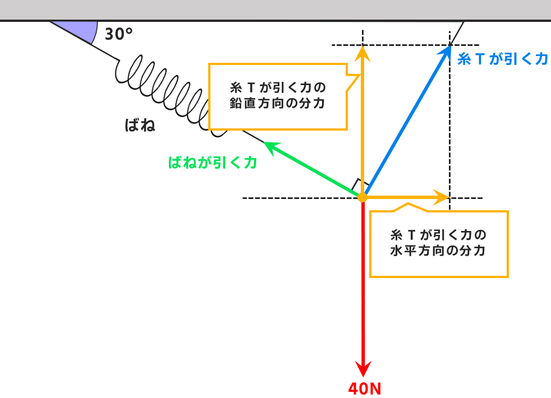
ここにも30度・60度・90度の三角形が隠れています。
糸Tが引く力をy(N)とすると

と表せます。↓

まとめると↓の図のようになります。
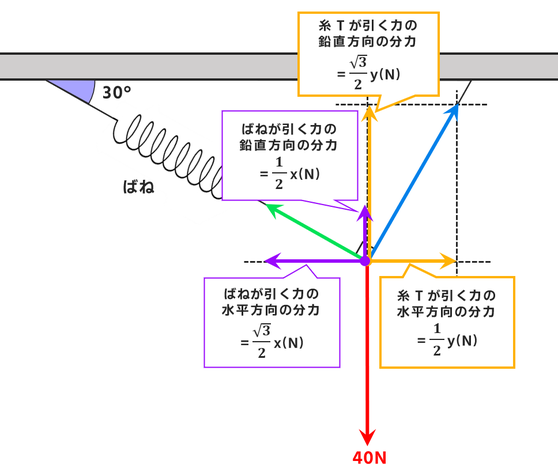
このとき
水平方向の力がそれぞれつり合い、鉛直方向の力もそれぞれつり合っているはず。
水平方向の力のつり合いから
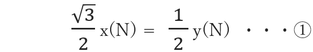
鉛直方向の力のつり合いから
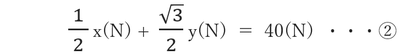
①・②をx・yに関する連立方程式で解くと
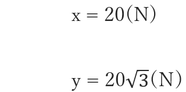
となります。
よって
糸Tにはたらく分力 = 20√3(N)
ばねにはたらく分力 = 20(N)
となります。
次回は「分力を使った力のつり合い2」です!

