1.分力と三平方の定理・相似
●力
単位は[N]。
力は矢印で表し、矢印の長さが力の大きさを表す。
例題1
↓の図のように30度の傾きを持つ三角形型の台に1kgの物体を置きました。
100gの物体にはたらく重力を1Nとすると、この物体には10Nの重力がはたらいていることになります。

この重力を斜面に平行な方向と垂直な方向に分解してみましょう。↓

すると↓の図のように
・斜面に平行な方向の分力
・斜面に垂直な方向の分力
が得られます。

ここで↓の図のような水色の三角形とピンクの三角形に注目します。

↓の図のようにこの三角形は
・直角の部分
・黄色の角の部分(平行線における同位角は等しいため)
の2組の角が等しいことになります。

つまり水色の三角形とピンクの三角形は相似なのです。
相似な図形の対応する角は等しいですよね。
よって↓の図の茶色の角はともに30度です。(ちなみに黄色の角は60度)

ここで30度・60度・90度の三角形と言えば・・・
その辺の比が1:2:√3ですよね。↓

力の大きさは矢印の長さで決まります。
先ほど重力を分解した部分では↓の図のような長さの関係があるのです。

つまり重力が10Nであるとすると
・斜面に平行な方向の分力=5N
・斜面に垂直な方向の分力=5√3N
となります。
例題2
今度は↓の図のような、
3辺が3m・4m・5mの長さの三角形の台に10kgの物体を置きました。

100gの物体にはたらく重力を1Nとすると、この物体には100Nの重力がはたらいていることに
なります。
先ほどと同様この重力を斜面に平行な方向と斜面に垂直な方向に分解してみましょう。

ここには相似な三角形が隠れています。
↓の図の水色の三角形とピンクの三角形です。(それぞれ茶色の角、黄色の角が等しい)

この相似の関係からピンクの三角形の辺の比も3:4:5になります。↓

力の大きさは矢印の長さで決まるので、重力を分解した部分では↓の図のような長さの関係が
あることになります。
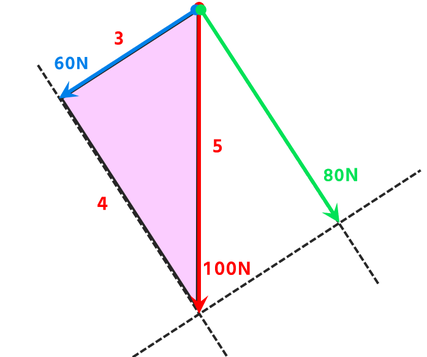
よって重力が100Nであるならば
・斜面に平行な方向の分力=60N
・斜面に垂直な方向の分力=80N
となります。
このように三角形の相似と三平方の定理を使うと分力を求めることができます。
よく登場するのは
・30度、60度、90度の直角三角形
・45度、45度、90度の直角二等辺三角形
・辺の長さの比が3:4:5の直角三角形
・辺の長さの比が5:12:13の直角三角形
の有名な直角三角形ばかりです。
・分力を求める時は三角形の相似と三平方の定理を使おう!
次回は「分力を使った力のつり合い」です!

